逻辑回归(二分类回归模型)
针对一个二分类问题,我们希望可以使用一个模型区别0,1. 但是直接得到0,1的话往往不太准确,但是得到倾向于0或者1的程度是多少能够得到更加准确的结果,也就是不直接得到0,1而是得到条件概率P(Y=1|X=x),P(Y=0|X=x),再给定阈值去判断倒到底是1还是0. 所以怎么才能在一个模型中,学习到变量的条件概率呢? 最简单的办法是用线性回归解决这个问题. 下面有几个方法:
- 拟合p(x)成线性方程
- p(x)在[0,1]区域之间,但是线性方程值域为实数域,不可能局限在[0,1],否决掉
- 拟合log p(x)成线性方程
- log p(x)在[-00,0]区域之间,同样的问题,否决掉
- 拟合log(p/(1-p))成线性方程
- p/(1-p)是几率, log(p/(1-p))是对数几率, 称为logistic/logit transformation, 这样的转换就没有值域上的限制了. 符合要求
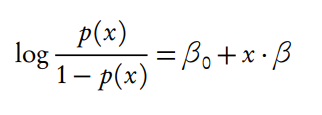 转换后得到:
转换后得到:
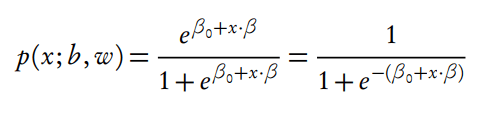 如果线性方程大于0, 概率为1, 线性方程小于0, 概率为0, 这样逻辑回归提供了一个线性分类器. 这样就可以得到两个分类的概率:
\[ P(Y = 1) = exp(wx) / (1 + exp(wx)) \]
\[ P(Y = 0) = 1 / (1 + exp(wx)) \]
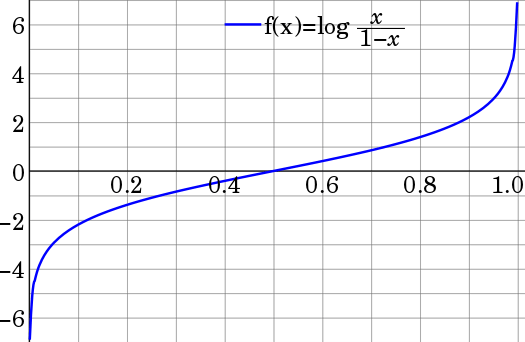
返回去看为什么log(p/(1-p))是一个比较好的转换,下面是log(p/(1-p))的分布图. p取中间的概率的情况, log(p/(1-p))变化很平缓,而p越靠近0或者1,log(p/(1-p))越趋向于负无穷和正无穷.
转化成上面两个式子,就是我们熟悉的sigmoid的解释: wx越大,概率越趋向与1,越小,概率越趋向于0. 而尽量中间情况wx取值很少. 这样才能构成一个更加准确的分类器.
如果线性方程大于0, 概率为1, 线性方程小于0, 概率为0, 这样逻辑回归提供了一个线性分类器. 这样就可以得到两个分类的概率:
\[ P(Y = 1) = exp(wx) / (1 + exp(wx)) \]
\[ P(Y = 0) = 1 / (1 + exp(wx)) \]
返回去看为什么log(p/(1-p))是一个比较好的转换,下面是log(p/(1-p))的分布图. p取中间的概率的情况, log(p/(1-p))变化很平缓,而p越靠近0或者1,log(p/(1-p))越趋向于负无穷和正无穷.
转化成上面两个式子,就是我们熟悉的sigmoid的解释: wx越大,概率越趋向与1,越小,概率越趋向于0. 而尽量中间情况wx取值很少. 这样才能构成一个更加准确的分类器.
所以说,逻辑回归是利用线性回归学习因变量概率的问题的模型, 从而逻辑回归变成一个模型选择的问题,针对不同的线性模型,可以得到不同效果的分类
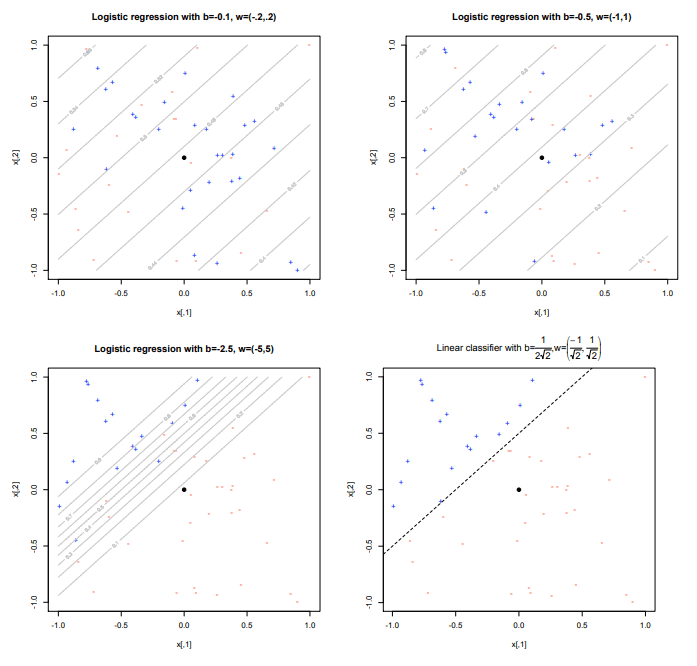
与线性回归的区别 (转自引文2)
- 线性回归要求变量服从正态分布,logistic回归对变量分布没有要求。
- 线性回归要求因变量是连续性数值变量,而logistic回归要求因变量是分类型变量。
- 线性回归要求自变量和因变量呈线性关系,而logistic回归不要求自变量和因变量呈线性关系
- logistic回归是分析因变量取某个值的概率与自变量的关系,而线性回归是直接分析因变量与自变量的关系
logistic回归与线性回归实际上有很多相同之处,最大的区别就在于他们的因变量不同,其他的基本都差不多, 正是因为如此,这两种回归可以归于同一个家族,即广义线性模型(generalizedlinearmodel)。 这一家族中的模型形式基本上都差不多,不同的就是因变量不同,如果是连续的,就是多重线性回归,如果是二项分布,就是logistic回归。 logistic回归的因变量可以是二分类的,也可以是多分类的,但是二分类的更为常用,也更加容易解释。 所以实际中最为常用的就是二分类的logistic回归。
Reference
- http://www.stat.cmu.edu/~cshalizi/uADA/12/lectures/ch12.pdf
- https://blog.csdn.net/gcs1024/article/details/77478404