激活函数
sigmoid和softmax函数的存在是将计算的logit转化为概率p。sigmoid用于二分类逻辑回归，softmax用于多分类逻辑回归。
sigmoid
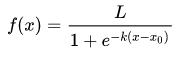求导：
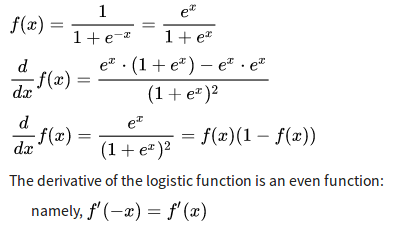
概率p的logit是\(L=\ln\frac{p}{1-p} \)。其中\(\frac{p}{1-p}\)是odd(两者比率)，logit反过来就是\(p= \frac{1}{1+e^{-L}}\)（sigmoid）
softmax
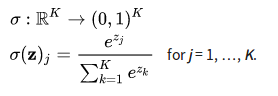可以看出，当二分类问题使用softmax，softmax公式就等于sigmoid公式。
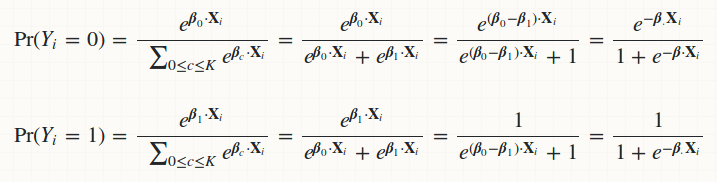
一个计算小技巧：
因为都是指数函数，所以分子和分母很有可能非常大，通过下面的转换，其中logC = -max(f)
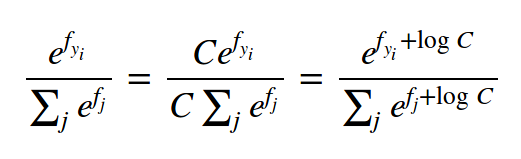
f = np.array([123, 456, 789]) # example with 3 classes and each having large scores
p = np.exp(f) / np.sum(np.exp(f)) # Bad: Numeric problem, potential blowup
# instead: first shift the values of f so that the highest number is 0:
f -= np.max(f) # f becomes [-666, -333, 0]
p = np.exp(f) / np.sum(np.exp(f)) # safe to do, gives the correct answer
损失函数（度量模型性能的方法）
均方误差，mean squared error
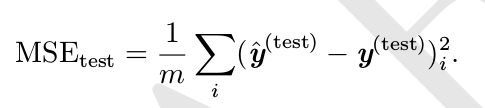
交叉熵
首先介绍一下熵。
一条消息的信息量等于他的不确定的多少。 假设要从32个足球队伍里面选择1个冠军队伍，我们可以猜5次就能决定是那一支。所以这个信息量为5（log32=5）。 但是有时候我们已经知道了不是每支队伍的取胜概率都一样，我们可以将厉害的几只队伍放在一起，剩下的直接排除，那么信息量就应该是\( H=-(p1*logp1+p2*logp2+…+p32*logp32)\) 所以信息熵的定义为\[ H(x)=-\sum(p(x)*log(p(x)))\] 也就是\[ H(p)=\sum_{i}^{} p(i)*log\frac{1}{p(i)} \]
所以熵的本质是香农信息量\(log\frac{1}{p} \)或者\( -log(p(x))\)的期望。
上面的p(x)是真实分布, 如果用错误分布q(x)来表示的话就是交叉熵H(p,q) \[ H(p,q)=\sum_{i}^{} p(i)*log\frac{1}{q(i)} \] 因为q的样本来自分布p，所以期望H(p,q)中概率是p(i)。
根据Gibbs’ inequality可知, H(p,q)>=H(p)恒成立. 可以理解为, 用错误分布来计算的信息熵一定会比正确分布计算的大. 只有当q等于正确分布的时候等号才成立.
我们将H(p,q)和H(p)的差异, 几多出来的那些信息熵叫做相对熵. 也称为KL散度(Kullback–Leibler divergence，KLD) . \[ D(p||q)=H(p,q)-H(p)=\sum_{i}^{} p(i)*log\frac{p(i)}{q(i)} \] KL散度是用来衡量两个分布的差异. 如果KL越小, 两个分布的差异越小, KL=0表示两个分布相等.
交叉熵可在神经网络(机器学习)中作为损失函数，p表示真实标记的分布，q则为训练后的模型的预测标记分布，交叉熵损失函数可以衡量p与q的相似性。交叉熵作为损失函数还有一个好处是使用sigmoid函数在梯度下降时能避免均方误差损失函数梯度消失的问题，因为梯度可以被输出的误差所控制。
所以评价一个模型，可以判断预测结果分布与真实结果分布的相对熵是否足够低。就是上面说相对熵, 那为什么都叫交叉熵损失的, 我理解的是: H(p)对于一个固定的样本来说, 其实是固定的, 所以H(p)是一个固定的值, 那么计算H(p,q)-H(p)最小的话, 可以理解为H(p,q)最小, 就是所说的交叉熵损失函数了.
比较
分类器和损失函数选择汇总
均方误差在使用基于梯度的优化方法时往往成效不佳。交叉熵作为损失函数还有一个好处是使用sigmoid函数之类的饱和输出单元时在梯度下降时能避免均方误差损失函数学习速率降低的问题，因为学习速率可以被输出的误差所控制。
tensorflow中有几种方式计算损失函数的方式：
sigmoid系列：
- tf.nn.sigmoid_cross_entropy_with_logits
- tf.nn.weighted_cross_entropy_with_logits
- tf.losses.sigmoid_cross_entropy
sigmoid通常只在二分类上使用，但是tensorflow中，如果各个类别相互独立，sigmoid函数可用于多分类（tf.nn.sigmoid_cross_entropy_with_logits）。 label可以是one-hot encoded或者soft class probabilites(概率比值) tf.nn.weighted_cross_entropy_with_logits tf.losses.sigmoid_cross_entropy 两个函数可以设置权重，这样有助于训练不平衡数据集。
softmax系列：
- tf.nn.softmax_cross_entropy_with_logits
- tf.losses.softmax_cross_entropy
适用于类别>=2的分类问题。label可以是one-hot encoded或者soft class probabilites(概率比值)。 tf.losses.sigmoid_cross_entropy同样可以添加权重。
spare系列：
- tf.nn.sparse_softmax_cross_entropy_with_logits
- tf.losses.sparse_softmax_cross_entropy
适用于类别>=2的分类问题。与softmax系列唯一的不同是label是class index的int，不是上面的one-hot encoded。tf.losses.sparse_softmax_cross_entropy同样可以设置权重。
Reference:
- https://stackoverflow.com/questions/47034888/how-to-choose-cross-entropy-loss-in-tensorflow
- 数学之美
- 深度学习
- https://jamesmccaffrey.wordpress.com/2013/11/05/why-you-should-use-cross-entropy-error-instead-of-classification-error-or-mean-squared-error-for-neural-network-classifier-training/
- http://cs231n.github.io/
- https://www.zhihu.com/question/41252833/answer/108777563
- https://www.zhihu.com/question/65288314/answer/244588905
